方法功能：获取指定整数转换成二进制后的前导零的个数。

比如数字3的二进制是0000 0000 0000 0000 0000 0000 0000 0011，那么可以得到它的前置0有30位，最后两位是11。

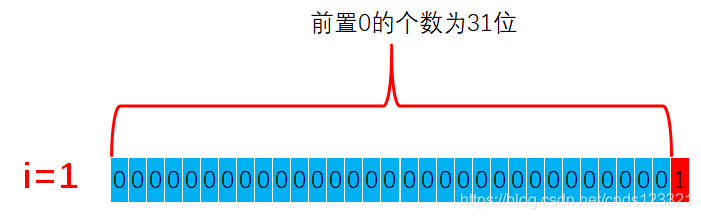
该方法的源码如下：

    /**
     * Returns the number of zero bits preceding the highest-order
     * ("leftmost") one-bit in the two's complement binary representation
     * of the specified {@code int} value.  Returns 32 if the
     * specified value has no one-bits in its two's complement representation,
     * in other words if it is equal to zero.
     *
     * <p>Note that this method is closely related to the logarithm base 2.
     * For all positive {@code int} values x:
     * <ul>
     * <li>floor(log<sub>2</sub>(x)) = {@code 31 - numberOfLeadingZeros(x)}
     * <li>ceil(log<sub>2</sub>(x)) = {@code 32 - numberOfLeadingZeros(x - 1)}
     * </ul>
     *
     * @param i the value whose number of leading zeros is to be computed
     * @return the number of zero bits preceding the highest-order
     *     ("leftmost") one-bit in the two's complement binary representation
     *     of the specified {@code int} value, or 32 if the value
     *     is equal to zero.
     * @since 1.5
     */
    public static int numberOfLeadingZeros(int i) {
        // HD, Figure 5-6
        if (i == 0)
            return 32;
        int n = 1;
        if (i >>> 16 == 0) { n += 16; i <<= 16; }
        if (i >>> 24 == 0) { n +=  8; i <<=  8; }
        if (i >>> 28 == 0) { n +=  4; i <<=  4; }
        if (i >>> 30 == 0) { n +=  2; i <<=  2; }
        n -= i >>> 31;
        return n;
    }

对该方法进行注释：

    /**
     * 回指定int值的二进制补码二进制表示形式中最高位（“最左端”）一位之前的零位数目。 如果指定值的二进制补码表示中没有一位（即等于零），则返回32。
     * 注意，此方法是密切相关的数底2对所有正int值x：
     * floor（log 2 （x））= 31 - numberOfLeadingZeros(x)
     * ceil（log 2 （x））= 32 - numberOfLeadingZeros(x - 1)
     * 比如数字3的二进制是0000 0000 0000 0000 0000 0000 0000 0011，那么可以得到它的前置0有30位，最后两位是11
     * 比如数字8的二进制是0000 0000 0000 0000 0000 0000 0000 1000，那么可以得到它的前置0有28位，最后四位是1000
     * 参考链接：https://blog.csdn.net/cnds123321/article/details/117338989
     *
     * @param i 要计算前导零个数的值
     * @return 指定的int值的二进制补码二进制表示形式中（"最左端"）一位之前的零位数目；如果该值等于0，则为32位
     */
    public static int numberOfLeadingZeros(int i) {
        // 如果传入的数是0，那么32位二进制一定都是0，所以直接返回32即可，不需要再进行下面的操作
        if (i == 0)
            return 32;
        // 局部变量，统计前导零的个数，初始值为1，即至少存在1个，因为0个情况已经被上面的if判断排除了
        int n = 1;
        // 这个思路就是二分查找，首先把32位的数分为高低16位，如果非零值位于高16位，后续再将高16位继续二分为高低8位，一直二分到集合中只有1个元素
        /*
            将i无符号右移16位后，有二种情况：
                第一种情况，i=0，则第一个非零值位于低16位，i至少有16个前导0，同时将i左移16位（把低16位移到原高16位的位置，这样情况1和情况2就能统一后续的判断方式）
                    例如：数字123的二进制是0000 0000 0000 0000  0000 0000 0111 1011，无符号右移16位后二进制是0000 0000 0000 0000  0000 0000 0000 0000，表明第一个非零值在低16位
                第二种情况，i!=0,则第一个非零值位于高16位，后续在高16位中继续判断
         */
        // 只是判断当i无符号右移16位后是否等于0，如果等于0则表示第一个非零值在低16位，如果不等于则表示第一个非零值在高16位
        if (i >>> 16 == 0) {
            // 执行到这里，表示第一个非零值在低16位，那么表示数字i的高16位全是0，也就是说至少有16个前导0，用n记录起来
            n += 16;
            // 既然i的第一个非零值在低16位，那么将i左移16位，将低16位移动到原来高16位的位置，继续判断
            // 例如：数字123的二进制是0000 0000 0000 0000  0000 0000 0111 1011，左移16位后二进制是0000 0000 0111 1011  0000 0000 0000 0000
            i <<= 16;
        }
        // 判断第一个非零值是否在高8位，如果i>>>24==0为true表示第一个非零值在低8位，为false表示在高8位
        if (i >>> 24 == 0) {
            // 执行到这里，表示第一个非零值在低8位，那么表示数字i的高8位全是0，也就是说至少有8个前导0，用n记录起来
            n += 8;
            // 既然i的第一个非零值在低8位，那么将i左移8位，将低8位移动到原来高8位的位置，继续判断
            // 例如：数字123的二进制是0000 0000 0000 0000  0000 0000 0111 1011
            // 左移16位后二进制是    0000 0000 0111 1011  0000 0000 0000 0000
            // 又左移8位后二进制是   0111 1011 0000 0000  0000 0000 0000 0000
            i <<= 8;
        }
        // 判断第一个非零值是否在高4位，如果i>>>28==0为true表示第一个非零值在低4位，为false表示在高4位
        if (i >>> 28 == 0) {
            // 执行到这里，表示第一个非零值在低4位，那么表示数字i的高4位全是0，也就是说至少有4个前导0，用n记录起来
            n += 4;
            // 既然i的第一个非零值在低4位，那么将i左移4位，将低4位移动到原来高4位的位置，继续判断
            // 例如：数字1的二进制是0000 0000 0000 0000  0000 0000 0000 0001
            // 左移16位后二进制是  0000 0000 0000 0001  0000 0000 0000 0000
            // 又左移8位后二进制是 0000 0001 0000 0000  0000 0000 0000 0000
            // 又左移4位后二进制是 0001 0000 0000 0000  0000 0000 0000 0000
            i <<= 4;
        }
        // 判断第一个非零值是否在高2位，如果i>>>30==0为true表示第一个非零值在低2位，为false表示在高2位
        if (i >>> 30 == 0) {
            // 执行到这里，表示第一个非零值在低2位，那么表示数字i的高2位全是0，也就是说至少有2个前导0，用n记录起来
            n += 2;
            // 既然i的第一个非零值在低2位，那么将i左移2位，将低2位移动到原来高2位的位置，继续判断
            // 例如：数字1的二进制是0000 0000 0000 0000  0000 0000 0000 0001
            // 左移16位后二进制是  0000 0000 0000 0001  0000 0000 0000 0000
            // 又左移8位后二进制是 0000 0001 0000 0000  0000 0000 0000 0000
            // 又左移4位后二进制是 0001 0000 0000 0000  0000 0000 0000 0000
            // 又左移2位后二进制是 0100 0000 0000 0000  0000 0000 0000 0000
            i <<= 2;
        }
        // i >>> 31是判断第一个非零值是否在高1位，如果在高1位则i>>>31得到的结果是1，如果在低1位则i>>>31得到的结果是0
        // n由于是从1开始的，所以这里需要减，如果是从0开始，就需要加
        n -= i >>> 31;
        // 返回统计的前导零个数
        return n;
    }

其实这个方法就是利用位运算求前导零的个数，思路就是不断进行二分来记录统计前导零的出现次数。

画了一个图，可能方便理解些：

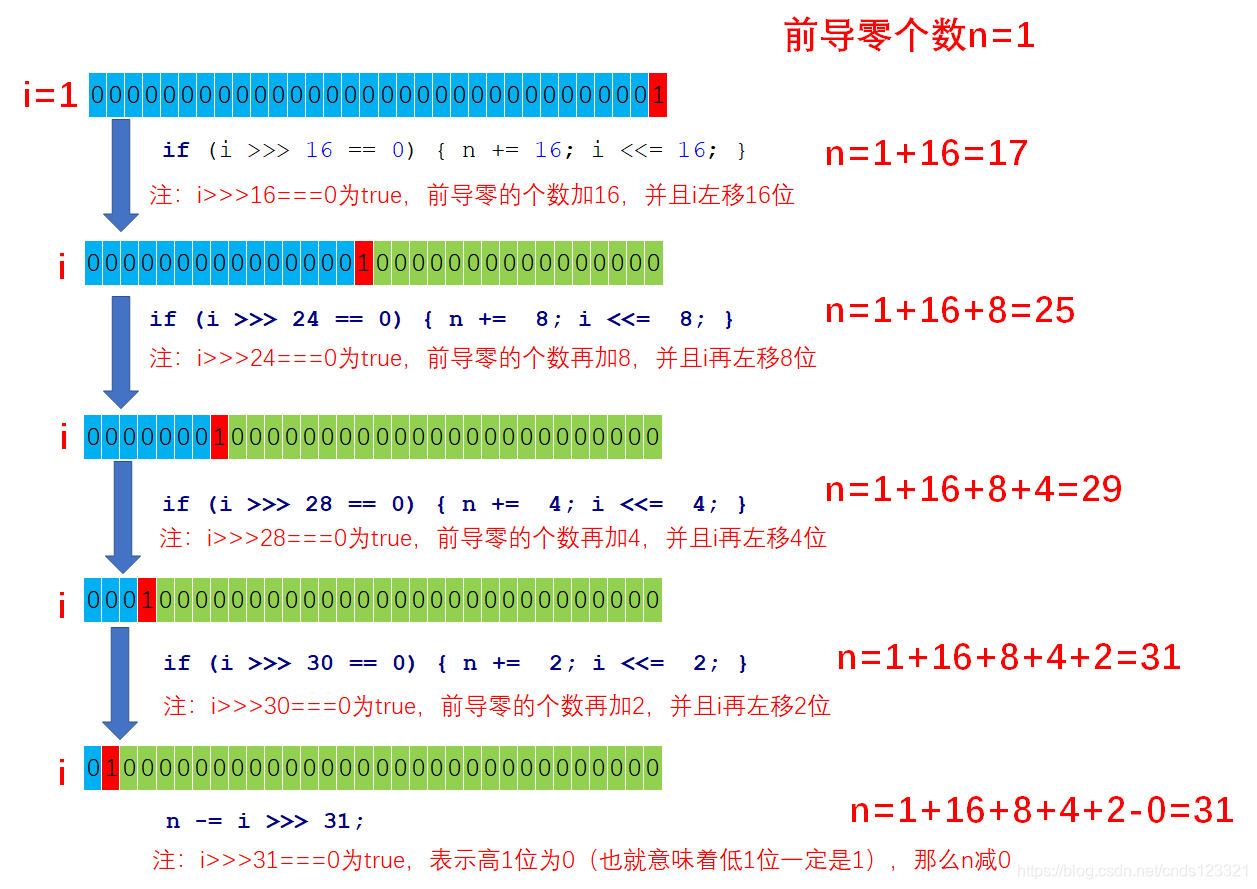
原文链接:https://blog.csdn.net/cnds123321/article/details/117338989